A) 40
B) 50
C) 60
D) 70
E) 80
Resolução:
Sabe-se que são 450 canditados no total e 80 não falam nem inglês e nem italiano. 280 falam inglês e 140 falam italiano. Na imagem abaixo você pode ver de forma organizada. O que você precisa é achar o valor do X como mostrado na imagem
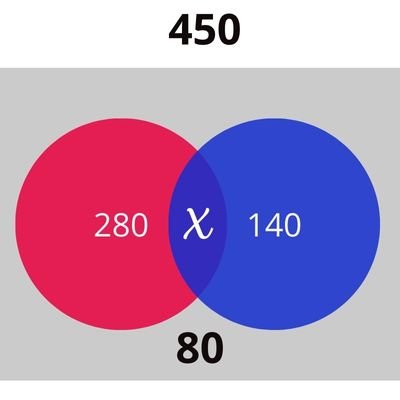
Veja que 450 é total de pessoas e 80 não falam nenhum dos idiomas citados, então 450 - 80 = 370. Esse é o número de pessoas que falam inglês ou italino. Como 280 falam ingles e 140 italiano, então 280 + 140 = 420 pessoas, mas sabe-se que há apenas 370 pessoas no circulo vermelho e azul, o que queremos saber é a intersecção entre o circulo vermelho e o verde, ou seja, o valor do X, então 420 - 370 = 50
A resposta é 50
Agora veremos como fazer os calculos usando matemática pura
Podemos resolver esse problema usando o princípio da inclusão e exclusão. Vamos denotar:
- ( A ): conjunto dos candidatos que falam inglês fluente.
- ( B ): conjunto dos candidatos que falam italiano fluente.
Então, estamos interessados em encontrar a interseção ( A ∩ B ), ou seja, os candidatos que falam ambas as línguas com fluência.
A fórmula para o princípio da inclusão e exclusão é dada por:
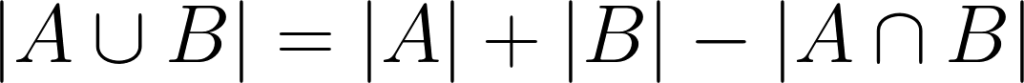
Onde ( |A ∪ B| ) é o número total de candidatos que falam pelo menos uma das línguas. Sabemos que 80 candidatos não falam fluentemente nenhuma das línguas, então:
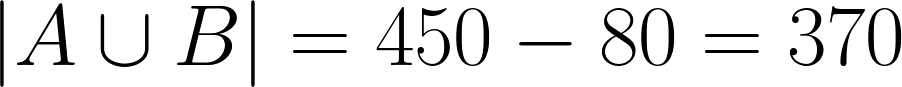
Também sabemos que ( |A| = 280 ) e ( |B| = 140 ). Substituindo esses valores na fórmula, obtemos:
Agora, resolvendo para ( |A ∩ B| ), temos:
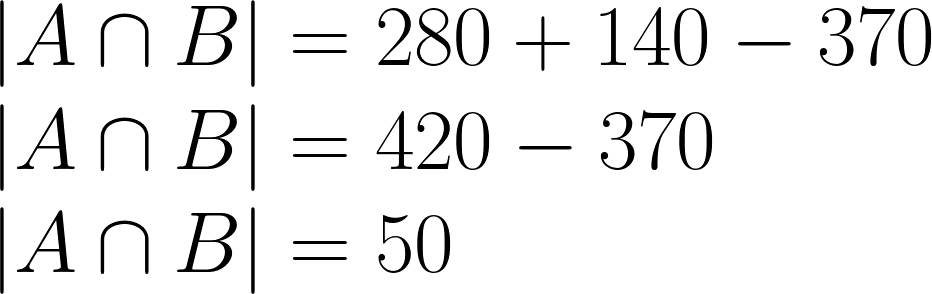
Portanto, há 50 candidatos que falam ambas as línguas com fluência.
Clique para ver mais sobre esse concurso na página do instituto aocp (editais e publicações)
Veja mais conteúdos como este aqui