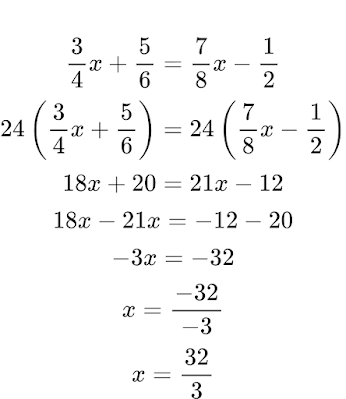Você sabe o que é e como resolver uma equação de 1º Grau? Nesse post veremos o que é uma equação de 1º Grau e como resolver. Uma equação de 1º grau tem essa forma:
$$ax+b=0$$
A letra "a" e "b" são números conhecidos, ou seja, quando você for resolver um problema com uma equação dessa os valores já serão anunciados. Com ''a'' diferente de 0 (a ≠ 0). Por que "a" não pode ser zero? Por que se for zero não pode ser uma equação de 1º grau. Observe na equação abaixo que se colocarmos 0 no lugar de "a" teremos $0 \times x$ que é igual a zero, assim resultaria em 3 = 4 que não é possível.
Ex.:
$$x+3=4$$
Na equação acima observe que $a=1$ e $b=3$, o valor de a não aparece justamente por que o valor é 1. Resolvendo essa equação podemos ver que o valor de x é 1. O valor 1 pode ser chamado de raiz ou solução. Então toda vez que você ouvir o termo "Ache a raiz ..." ou "Ache a solução ..." Então saiba que o enunciado está pedindo para você resolver o "x", mas tome cuidado pois nem sempre é "x", as vezes pode ser z, y, w ou até mesmo o desenho de um elefante.
Ex.:
O conjunto S = {4} é o conjunto solução da equação.
Toda equação tem uma letra que indica um número desconhecido. A letra é chamada de incógnita da equação. Por exemplo: 3x+4=8, a incógnita é x. Numa equação a letra x representa um número,não importa se no lugar de x está a letra z, b, f, t, h, ou qualquer letra.
Numa equação, a expressão que vem à esquerda do sinal = é chamada de 1º membro; a da direita é o 2º membro.
Para resolvermos uma equação usamos a operação inversa, ou seja, o número que está com o sinal de menos (-) passa para o outro lado com o sinal de mais (+). Se algum número está multiplicando, uma letra, ele passa para o outro lado dividindo. Exemplo: 2x = 10 → x = 10/2. Observe que 2 está multiplicando x, o 2 passou para o outro lado dividindo. A operação inversa de multiplicação é divisão e de subtracão é adição.
Ao resolver uma equação o que mais queremos saber é o valor de x. Resolver uma equação é deixar ambos os membros iguais. Observe no exemplo ① que se subtrairmos -4 de cada lado veremos que o valor de x = 2. Para ter certeza de que x realmente vale 2 substituiremos esse 2 na 1ª linha. O resultado será 6=6 então está certo.
① Passe o 4 do 1º membro para o 2º membro com o sinal inverso. $$4+x=6$$$$x=6-4$$$$x=2$$
⑤
Ex.:
$$x+3=4$$
Na equação acima observe que $a=1$ e $b=3$, o valor de a não aparece justamente por que o valor é 1. Resolvendo essa equação podemos ver que o valor de x é 1. O valor 1 pode ser chamado de raiz ou solução. Então toda vez que você ouvir o termo "Ache a raiz ..." ou "Ache a solução ..." Então saiba que o enunciado está pedindo para você resolver o "x", mas tome cuidado pois nem sempre é "x", as vezes pode ser z, y, w ou até mesmo o desenho de um elefante.
Ex.:
$3x+5=17$
$3x = 17 -5$
$x = \frac{12}{3}$
$x = 4$
A raiz é 4, então S = {4}O conjunto S = {4} é o conjunto solução da equação.
COMO RESOLVER UMA EQUAÇÃO DE 1º GRAU
Toda equação tem uma letra que indica um número desconhecido. A letra é chamada de incógnita da equação. Por exemplo: 3x+4=8, a incógnita é x. Numa equação a letra x representa um número,não importa se no lugar de x está a letra z, b, f, t, h, ou qualquer letra.
Numa equação, a expressão que vem à esquerda do sinal = é chamada de 1º membro; a da direita é o 2º membro.
Cada parcela, do 1º e do 2º membro, é chamada de termo.
Para resolvermos uma equação usamos a operação inversa, ou seja, o número que está com o sinal de menos (-) passa para o outro lado com o sinal de mais (+). Se algum número está multiplicando, uma letra, ele passa para o outro lado dividindo. Exemplo: 2x = 10 → x = 10/2. Observe que 2 está multiplicando x, o 2 passou para o outro lado dividindo. A operação inversa de multiplicação é divisão e de subtracão é adição.
Ao resolver uma equação o que mais queremos saber é o valor de x. Resolver uma equação é deixar ambos os membros iguais. Observe no exemplo ① que se subtrairmos -4 de cada lado veremos que o valor de x = 2. Para ter certeza de que x realmente vale 2 substituiremos esse 2 na 1ª linha. O resultado será 6=6 então está certo.
① Passe o 4 do 1º membro para o 2º membro com o sinal inverso. $$4+x=6$$$$x=6-4$$$$x=2$$
No exemplo ② e ③ foi feito o mesmo processo que no exemplo ①. Pra começar a resolver vamos isolar o x, pra isso vamos separar os números e os números com a letra x. Observe que na 2ª linha de ② o +8 passou para o outro lado da igualdade transformado em -8. Na 3ª linha o -2 vai para o outro lado dividindo o 10.
② $$-2x+8=18$$$$-2x=18-8$$$$-2x=10$$$$x=\frac{10}{-2}$$$$x=-5$$
③$$10x+4=3x+25$$$$10x-3x=25-5$$$$7x=21$$$$x=3$$
② $$-2x+8=18$$$$-2x=18-8$$$$-2x=10$$$$x=\frac{10}{-2}$$$$x=-5$$
③$$10x+4=3x+25$$$$10x-3x=25-5$$$$7x=21$$$$x=3$$
No exemplo ④ multiplique ambos os lados por 4 para que o denominador da fração x/4 seja eliminado e se torne um número inteiro.
④$$\frac{x}{4}=3$$$$x=3 \times 4$$$$x=12$$
No exemplo ⑤ é feito o mesmo processo que no exemplo ④. Mas como nos denominadores há vários números diferentes em cada fração é necessário tirar o mmc e multiplicar ambos os lados pelo resultado do mmc.⑤
No exemplo ⑥ basta desenvolver a equação. Multiplique o número pelo o que está dentro dos parenteses.
⑥$$7(x-3)=2(x+1)$$$$7x-21=2x+2$$$$7x-2x=21+2$$$$5x=23$$$$x=\frac{23}{5}$$
No exemplo ⑦ é igual o exemplo ⑤. Tire o mmc e multiplique ambos os lados pelo resultado para que se torne números inteiros.
⑦$$\frac{2x+3}{2}=\frac{x-1}{4}$$$$4\left(\frac{2x+3}{2}\right)=4\left(\frac{x-1}{4}\right)$$$$2(2x+3)=x-1$$$$4x+6=x-1$$$$4x-x=-1-6$$$$3x=-7$$$$x=-\frac{7}{3}$$
Veja que não é complicado. As equações de 1º grau é apenas achar o valor da incógnita. Claro que nesse post o objetivo era explicar apenas como achar essa incógnita e te dar uma base do que é uma equação de 1º grau. Quando você estudar "função de 1º grau e gráficos" verá que é um pouco mais complexo, mas ao mesmo tempo é muito gostoso passar o tempo estudando isso.
Alguma dúvida, sugestão? Faça um comentário, sua interação é muito importante aqui!
Se gostou não se esqueça de compartilhar: